算法导论第6,7,8,9章习题答案
6.5-6
Q:说明如何使用优先级队列来实现一个先进先出队列,另说明如何用优先级队列来实现栈。
A:队列的性质是先进先出,所以维护一个最小优先级队列,给先进队的元素赋一个小的优先级,每插入一个新的元素优先级加1。 出队时取优先级最小的元素并维护优先级队列即可。栈的实现同理。
6.5-7
Q:HEAP-DELETE(A,i)操作将结点i中的项从堆A中删去。对含n个元素的最大堆,请给出时间为O(lgn)的HEAP-DELETE的实现。
A:类似于堆排序时做的操作,将要删除的结点和堆的最后一个结点交换,将其删除后维护堆的性质。伪代码:
HEAP-DELETE(A,i)
{
A[i] = A[heap-size[A]];
heap-size[A] = heap-size[A] - 1;
key = A[i];
if key <= A[PARENT[i]] then //放在i位置的新元素应该在堆更下面的位置
MAX-HEAPIFY(A,i);
else //放在i位置的新元素应该在堆更上面的位置
while i>1 and A[PARENT(i)] < key do
{
A[i] = A[PARENT[i]];
i = PARENT(i);
}
}
6-3 Young氏矩阵
Q:一个 m x n 的Young氏矩阵(Young tableau)是一个 m x n 的矩阵,其中每一行的数据都从左到右排序,每一列的数据都从上到下排序。 Young氏矩阵中可能会有一些 ∞ 的数据项,表示不存在的元素。所以,Young氏矩阵可以用来存放 r <= mn个有限的数。请给出一个运行时间为O(m+n)的算法, 来决定一个给定的数是否存在于一个给定的 m x n 的Young氏矩阵内。
A:我们可以用给定的数和Young氏矩阵中最右上角的那个数比,如果给定的数比较大,则该数不可能存在于最上面那行;如果给定的数比较下,那么该数不可能存在于最右边那列。 这样每次比较就可以排除一行或者一列。重复此过程,直到找到给定的数或者所有的行和列都被排除了为止。伪代码:
Search-Young(A,i,j,x)
{
if x = A[i,j] then return true;
if x > A[i,j] then
if i < m then return Search-Young(A,i+1,j,x);
else return false;
if x < A[i,j] then
if j > 1 then return Search-Young(A,i,j-1,x);
else return false;
}
main()
{
Search-Young(A,1,n,x);
}
7-6 对区间的模糊排序
Q:考虑这样一种排序问题,即无法准确的知道等排序的各个数字到底是多少。对于其中的每个数字,我们只知道它落在实轴上的某个区间内。 亦即,给定的n个形如[ai, bi]的闭区间,其中ai ≤ bi。算法的目标是对这些区间进行模糊排序(fuzzy-sort),亦即, 产生各区间的一个排序 <i1, i2, i3, i4,…in >,使得存在一个 cj ∈[ai, bi],满足c1≤c2≤…≤cn。
为n个区间的模糊排序设计一个算法,你的算法应该具有算法的一般结构,它可以快速排序左部端点(即各ai), 也要能充分利用重叠区间来改善运行时间。(随着各区间重叠得越来越多,对各区间的排序的问题会变得越来越容易,你的算法应该能充分利用这种重叠。)
A:算法的思想是仿照快速排序对各个区间进行排序,不同的地方,也是本题的关键在于如何利用重叠区间来改善运行时间。
很容易可以想到,如果两个区间有重叠,那么它们之间的顺序可以是任意的,即可以将这两个区间视作相等。对于区间[ai,bi],[aj,bj],有下列三种情况:
1> if (bi<aj) then [ai,bi]<[aj,bj]
2> else if (ai>bj) then [ai,bi]>[aj,bj]
3> else [ai,bi] = [aj,bj]
算法与快速排序稍有不同,由于可能存在许多相等的区间,我们改为三路快速排序,即每次partition进行划分时, 将区间分为三类,左边部分是小于pivot的,中间一部分是等于pivot的,右边部分是大于pivot的。 由于中间的那一部分里的所有区间相等,则它们必须存在同一段公共的重叠部分,所以pivot的选取要特别注意。
我们首先选取一个区间作为pivot,然后在划分时,如果有某个区间和pivot有重叠,则将其加入中间的那一部分,然后提取重叠区域作为新的pivot继续划分。伪代码:
fuzzy-sort(Intervals,beg,end)
{
if beg < end then
{
(p,q) = partition(Intervals,beg,end); //p,q为将区间数组分割为三部分的两个分界
fuzzy-sort(Intervals,beg,p-1);
fuzzy-sort(Intervals,q+1,end);
}
}
partition(Intervals,beg,end)
{
pivot = Intervals[end];
p = beg-1;
q = end+1;
i = beg;
while (i<q) do
{
if Intervals[i].b < pivot.a then //当前区间小于pivot
{
p = p+1;
exchange(Intervals[p],Intervals[i]);
i = i+1;
}else if Intervals[i].a > pivot.b then //当前区间大于pivot
{
q = q-1;
exchange(Intervals[q],Intervals[i]);
}else //当前区间等于pivto,需要更新pivot的范围值
{
pivot.a = max(pivot.a,Intervals[i].a);
pivot.b = max(pivot.b,Intervals[i].b);
i = i + 1;
}
}
return (p,q);
}
8.2-4
Q:请给出一个算法,使之对于给定的介于0到k之间的n个整数进行预处理,并能在O(1)时间内,回答出输入的整数中有多少个落在区间[a..b]内。你给出的算法的预处理时间应该是O(n+k)。
A:同计数排序的预处理一样,用一个数组C,C[i]保存小于等于i的整数的个数,那么在[a..b]范围内的整数个数就为C[b]-C[a] + (等于a的整数的个数)。
8.4-4
Q:在单位圆内有n个点,pi=(xi, yi),使得0<xi^2 + yi^2 ≤1, i = 1,2,....,n。 假设所有点是均匀分布的,亦即,某点落在圆的任一区域中的概率与该区域的面积成正比。 请设计一个Θ(n)期望的算法,来根据点到原点的距离di=sqrt(xi^2 + yi^2)对n个点排序。
A:题目给的提示是在桶排序算法中,设计适当的桶尺寸,以反映各个点在单位元中的均匀分布。 那么我们只需要把单位圆划分成n个面积相等的同心圆(环)即可。
把一个圆化为n个面积相等的同心圆(环),则每个圆(环)的面积为1/n。很容易得出各个圆环的半径Rk=sqrt(k/npi)。
8-3 排序不同长度的数据项
Q:a)给定一个整数数组,其中不同的整数中包含的数字个数可能不同,但是该数组中,所有整数中总的数字数为n。说明如何在O(n)时间内对该数组进行排序。
b)给定一个字符串数组,其中不同的串包含的字符个数可能不同,但所有串中总的字符个数为n。说明如何在O(n)时间内对该数组进行排序。 (注意此处的顺序是指标准的字母顺序,例如,a < ab < b)
A:a)先用计数排序算法按数字位数排序O(n),再用基数排序的方法分别对每个桶中的元素排序O(n)。
b)递归使用计数排序,先依据第一个字母进行排序,首字相同的放在同一组,再对每一组分别使用计数排序的方法比较第二个字母。以此类推。
8-4 水壶
Q:假设给定了n个红色的水壶和n个蓝色的水壶,它们的形状和尺寸都不相同。 所有红色水壶中所盛水的量都不一样,蓝色水壶也是一样。此外,对于每个红色的水壶, 都有一个对应的蓝色水壶,两者所盛的水量是一样的。反之亦然。 你的任务是将所盛水量一样的红色水壶和蓝色水壶找出来。为了达到这一目的,可以执行如下操作: 挑选出一对水壶,其中一个是红色的,另一个是蓝色的:将红色水壶中倒满水;再将水倒入到蓝色的水壶中。 通过这个操作,可以判断出来这两只水壶的容量哪一个大,或者是一样大。假设这样的比较需要一个时间单位。 你的目标是找出一个算法,它通过执行最少次数的比较,来确定分组和配对问题。记住不能直接比较两个红色的或两个蓝色的水壶。
给出一个随机化的算法,其期望的比较次数为O(nlgn)。
A:由于每个红色水壶和蓝色水壶都有一组配对,所以只需要对两组水壶分别排序即可。但是不允许直接比较两个相同颜色的水壶。 这里采用快速排序的思想,先从红色的水壶中随机选择一个作为蓝pivot,然后在蓝色水壶中查找和该红色水壶容量一样的那个做红pivot。 利用红pivot对蓝色水壶进行partition,再用蓝pivot对红色水壶进行partition。其余过程类似于快速排序。
8-5 平均排序
Q:假设我们不是要排序一个数组,而只是要求数组中的元素一般情况下都是层递增序的。 更准确地说,称一个包含n个元素的数组A为k排序的(k-sorted),如果对所有i=1,2, ..., n-k,有下式成立:
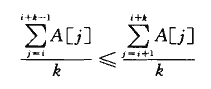
a)给出一个算法,它能在O(nlg(n/k))时间内,对一个n元素的数组进行k排序。
b)说明一个长度为n的k排序的数组可以在O(nlgk)内排序。
A:a)容易证明,一个n元素的数组是k排序的,当且仅当对所有i=1,2, .... n-k 有 A[i] ≤ A[i+k]。
所以我们只需要将该数组分为k个独立的小组,每个分组大小为n/k。 每个大小为n/k的分组进行排序的时间复杂度为O(n/k*lg(n/k)), 那么k个分组总的时间复杂度为k*O(n/k*lg(n/k)) = O(nlg(n/k))。
b)在a中对k个分组用一个k元素的最小堆进行k路合并,每次提取最小值和增加一个新元素的时间复杂为O(lgk)。 总共需要n次提取最小值和增加新元素的操作,则对应的时间复杂度为O(nlgk)。
9.1-1
Q:利用 n+lgn-2 次比较,找到n个元素中的第2小元素。
A:这道题的方法略难想,看了别人的解法,自己解释不清楚。这里附一个参考的链接。
9.3-5
Q:假设已经有了一个用于求解中位数的“黑箱”子程序,它在最坏情况下需要线性运行时间。 写出一个能解决任意顺序统计量的选择问题的线性时间算法。
A:算法类似于快速排序的partition,只是每次pivot的选择可以用“黑箱”程序求出的中位数。 假设“黑箱”程序为median(A,p,q),伪代码:
Select(A,p,q,i)
{
pivot = median(A,p,q);
if i == (p+q)/2 - p + 1 return pivot;
Partition A[p..q] around pivot;
if i < (p+q)/2 then
return Slelct(A,p,(p+q)/2,i);
else
return Select(A,(p+q)/2,q,i-(p+q)/2);
}
9.3-6
Q:对一个含有n个元素的集合来说,所谓k分位数(the kth quantile),就是能把已排序的集合分成k个大小相等的集合的k-1个顺序统计量。 给出一个能列出某一集合的k分位数的O(nlgk)时间的算法。
A:将n个元素划分为k个大小相等的集合,那么每个集合的元素个数为t=n/k,则题目要求的就是这n个元素中第t,2t,...,(k-1)t大的数。
如果按顺序依次求这k-1个数需要的时间为(k-1)*n。我们可以理由二分法来改进,首先查找第(k/2)个分位数, 然后以这个分位数为pivot将n个元素分为两段,分别对这两段用同样的方法来找其他分位数。可以将时间降为O(nlgk)。
9.3-7
Q:给出一个O(n)时间的算法,在给定一个有n个不同数字的集合S以及一个正整数 k<=n 后,它能确定出S中最接近其中位数的k个数。
A:首先找到S中的中位数,然后计算S中每个数与中位数差的绝对值,存于另一个数组A中;求出A中第k小的数x, 最后通过找出S中与中位数的差的绝对值小于x的数即为所求。
9.3-8
Q:设X[1..n]和Y[1..n]为两个数组,每个都包含n个已排好序的数。给出一个求数组X和Y中所有2n个元素的中位数的、O(lgn)时间的算法。
A:我们先假设所求的中位数在X里,为X[k]。在数组X中,X[k]比X[1..k-1]这k-1个数大,比X[k+1..n]这n-k个数小。 那么如果X[k]两个数组共同的中位数,那么X[k]必须必Y中的n-k个数大、比k-1个数小,即 Y[n-k] <= X[k] <= Y[n-k+1]。 我们可以用这个方法检查X[k]是否就是所求的中位数。
如果X[k]比Y[n-k+1]还大,那么说明在X中比X[k]大的数X[k+1..n]都不符合条件;如果X[k]比Y[n-k]还小,那么说明X中比X[k]小的数X[1..k-1]都不符合条件。 利用二分法,每次可以排除一半的数。如果在X中找不到,那么再反过来在Y中以同样的方法查找。伪代码:
TWo-ARRAY-MeDIAN(X,Y)
{
median = Find-Median(X,Y,n,1,n);
if median = NOT_FOUND then
median = Find-Median(Y,X,n,1,n);
retrun median;
}
Find-Median(X,Y,n,low,high)
{
if low > high then
return NOT_FOUND;
else
{
k = (low+high)/2;
if k=n and X[n]<=Y[1] then
return X[n];
else
{
if k<n and Y[n-k]<=X[k]<=Y[n-k+1] then
return X[k];
if X[k] > Y[n-k+1] then
return Find-Median(X,Y,n,low,k-1);
if X[k] < Y[n-k] then
return Find-Median(X,Y,n,k+1,high);
}
}
}
在网上还看到一个更加巧妙的改进:
递归求解该问题,解题规模不断减半,最后剩下4个元素时,得到问题的解。 分别取两个数组的中值midA和midB进行比较。 如果midA=midB,那么这个值就是结果。 否则,小的那个所在的数组去掉前面一半,大的那个去掉后面一半。 (对于两个数组的中值,共有n-1个元素,有n个元素比它大。但是对于min(minA,minB),最多只有n-2个元素比它小,所以一定不是所求的结果,同理去掉大的一半)。 然后对剩余的两个数组,用同的方法求它们的中值,直到两个数组一共剩下4个元素。
9.3-9
Q:Olay教授是一家石油公司的顾问,这家公司正在计划建造一条由东向西的大型管道,它穿过一个有n口油井的油田。 从每口井中都有一条喷油管道沿最短路径与主管道直接连接(或南或北),如下图所示。给定各口井的x坐标和y坐标, 应如何选择主管道的最优位置(使得各喷管长度总和最小的位置)?
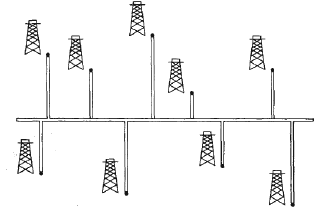
A:第一感觉是求中位数,但是也不知道为什么。百度了一下,看到一个非常好的解释:
为了简化这道题,不考虑油井的x坐标,假设所有的油井都在一条与管道垂直的线上。 假如有两个油井AB,分别在管道l的上下,那么不管这条管道在什么位置(只要在AB之间),d[Al]+d[bl]=d[AB]。 根据以上规律,把每两个油井分为一组,第i组中的油井是(y坐标第i大的油井和第i小的油井),只要管道在每组的两个油井之间,就能保证长度总和最小。
设所有油井的y坐标(较小的)中位数为yi,由以上推理得出答案:
1>如果油井的个数是奇数,让管道过yi位置。
2>如果点的个数是偶数,让管道位于yi和yi+1之间的任意位置(包括这两点)。
9-1 已排序的i个最大数
Q:给定一个含n个元素的集合,我们希望能用一个基于比较的算法来找出按顺序排列的i个最大元素。 请找出能实现下列每一种方法的、具有最佳的渐进最坏情况运行时间的算法,并分析各种方法的运行时间。
A:a)对输入数排序,并列出i个最大的数。 排序算法最优为O(nlgn)。
b)对输入数建立一个优先级队列,并调用EXTRACT-MAX过程i次。 建堆O(n) + i次EXTRACT-MAX 为 O(n+i*lgn)。
c)利用一个顺序统计量算法来找到第i个最大元素,然后换分输入数组,再对i个最大数排序。 划分O(n) + i个数排序O(ilgi) 为O(n+ilgi)。
9-2 带权中位数
Q:求n个元素的带权中位数。
(因为不好打公式,这里我就大概解释一下什么是带权中位数。n个元素x1,x2,...,xn分别具有一个正的权重w1,w2,...,wn,且权重和为1。 带权中位数xk要满足比xk小的元素的权重和小于1/2,并且比xk大的元素的权重小于等于0.5)
A:方法1,先对n个元素进行排序,然后从头开始依次对每个元素进行验证,同时累加权重,看其满足不满足带权中位数的条件。该算法的复杂度为排序的O(nlgn)+验证的O(n)。
方法2,类似于快速排序中的partition,用中位数进行分割,然后累加一边的权重和,看其满足带权中位数的条件否,不满足的话舍去一半继续递分割查找。伪代码:
Find-w-Median(X,start,end,w)
{
pivot = Find-Median(X,start,end);
Partition X(from start to end) around pivot;
if (sum of weight start...mid-1 < w) and (sum of weight start...mid >= w) then
return pivot;
else if (sum of weight start...mid-1 >= w) then
return Find-w-Median(X,start,mid-1,w);
else
return Find-w-Median(X,mid+1,end,w - sum of weight start...mid);
}
main()
{
return Find-w-Median(X,1,n,1/2);
}
这道题后面还附了一个带权中位数的应用问题:
邮局位置问题
Q:邮局位置问题(post-office location problem)定义如下:已知n个点p1,p2,...,pn及与他们相联系的权重w1,w2,...,wn。 我们希望找到一点p(不一定是输入点中的一个),使sum(wi*d(p,pi)) (i=1...n) 最小,此处d(a,b)表示点a与b之间的距离。
a)证明带权中位数是一维邮局位置问题的最佳解决方案,d(a,b) = | a-b | 。
b)找出二维邮局问题的最佳解决方案,其中所有的点都是(x,y)坐标对,并且d(a,b) = | xa-xb | + | ya-yb | 。
A:a)严格的证明不太会,这里给出一种容易理解的说明。假设各个点的权重都是整数的比例关系(同时将权重扩大足够大的倍数即可看出), 那么通过将每个点复制其权重比例多个,一维邮局问题则变为9.3-9描述的输油管道问题。按照9.3-9中配对的想法,中位数一定是带权中位数复制后中的一个。
b)将x坐标和y坐标分别求一维邮局问题,得到的坐标对即为二维邮局问题的解。
